Il y a des doutes sur la précision de la plupart des données statistiques, y compris lorsque les procédures sont suivies et qu'un équipement efficace est utilisé pour les tests. Excel vous permet de calculer l'incertitude en fonction de l'écart type de votre échantillon.
Il existe des formules statistiques dans Excel que nous pouvons utiliser pour calculer l'incertitude. Et dans cet article, nous calculerons la moyenne arithmétique, écart type et erreur type. Nous verrons également comment nous pouvons tracer cette incertitude dans un graphique dans Excel.
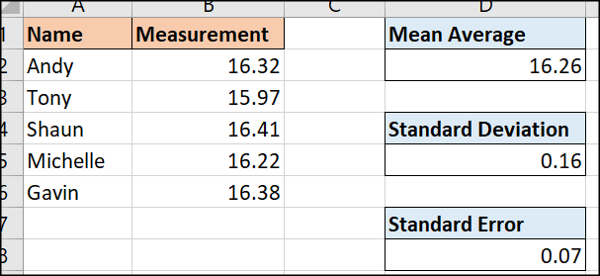
Nous utiliserons les exemples de données suivants avec ces formules.
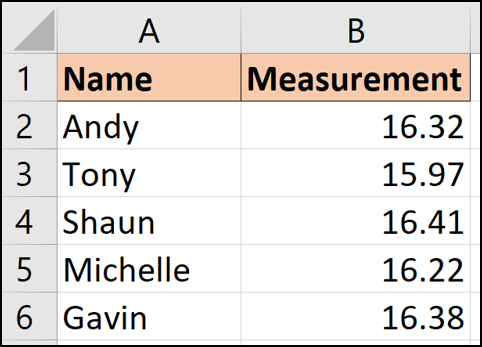
Ces données montrent cinq personnes qui ont pris une mesure ou une lecture quelconque. Avec cinq lectures différentes, nous ne savons pas quelle est la valeur réelle.
Moyenne arithmétique des valeurs
Lorsque vous n'êtes pas sûr d'une plage de valeurs différentes, prendre la moyenne (moyenne arithmétique) peut servir d'estimation raisonnable.
C'est facile à faire dans Excel avec la fonction MOYENNE.
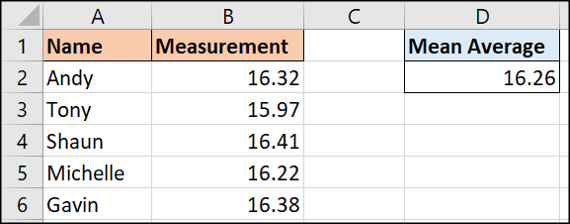
Nous pouvons utiliser la formule suivante sur les exemples de données ci-dessus.
= MOYENNE(B2:B6)
Écart type des valeurs
Les fonctions d'écart type montrent à quel point vos données sont réparties à partir d'un point central (la valeur moyenne moyenne que nous avons calculée dans la dernière section).
Excel a quelques fonctions d'écart-type différentes à des fins diverses. Les deux principaux sont STDEV.P et STDEV.S.
Chacun d'eux calculera l'écart type. La différence entre les deux est que STDEV.P s'appuie sur vous donner l'ensemble de la population de valeurs. STDEV.S fonctionne avec un échantillon plus petit de cette population de données.
Dans cet exemple, nous utilisons nos cinq valeurs dans l'ensemble de données, nous allons donc travailler avec STDEV.P.
Cette fonction fonctionne de la même manière que MOYENNE. Vous pouvez utiliser la formule suivante dans cet exemple de données.
=STDEV.P(B2:B6)
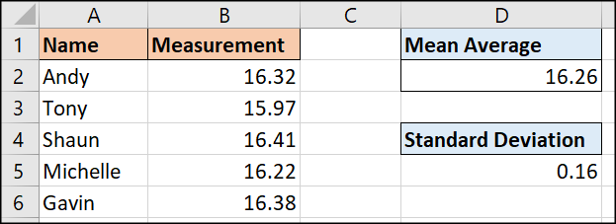
Le résultat de ces cinq valeurs différentes est 0,16. Ce nombre nous indique à quel point chaque mesure est différente de la valeur moyenne..
Calculer l'erreur standard
Avec l'écart type calculé, maintenant nous pouvons trouver l'erreur standard.
L'erreur type est l'écart type divisé par la racine carrée du nombre de mesures.
La formule suivante calculera l'erreur standard dans nos données d'échantillon.
=D5/SQRT(COMPTER(B2:B6))
Utilisation de barres d'erreur pour présenter l'incertitude dans les graphiques
Excel simplifie merveilleusement le tracé des écarts types ou des plages d'incertitude sur les graphiques. Nous pouvons le faire en ajoutant des barres d'erreur.
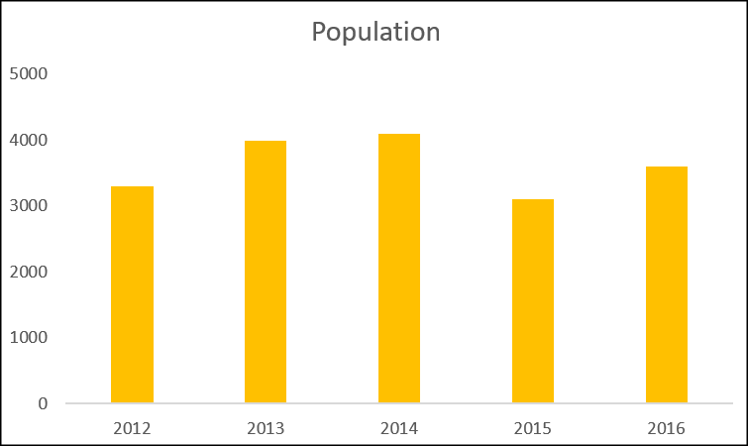
Ensuite, nous avons un histogramme d'un exemple d'ensemble de données montrant une population mesurée sur cinq ans.
Avec le graphique sélectionné, cliquez sur Conception> Ajouter un élément de graphique.
Plus tard, choisir parmi les différents types d'erreurs disponibles.
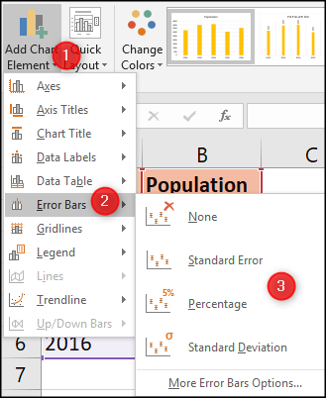
Il peut afficher une erreur standard ou un écart type pour toutes les valeurs, comme nous l'avons précédemment calculé dans cet article. Il peut également afficher un pourcentage de changement d'erreur. La valeur par défaut est 5%.
Pour cet exemple, nous choisissons d'afficher le pourcentage.
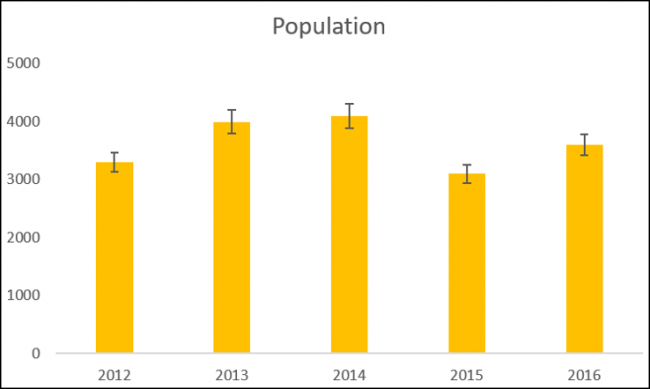
Il y a quelques autres options à explorer pour personnaliser vos barres d'erreur.
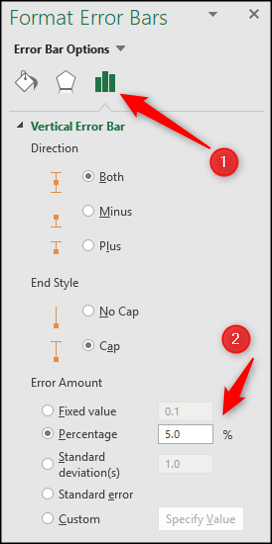
Double-cliquez sur une barre d'erreur dans le graphique pour ouvrir le panneau Format des barres d'erreur. Choisir une catégorie “Options des barres d'erreur” si pas déjà sélectionné.
Plus tard, vous pouvez ajuster le pourcentage, la valeur de l'écart type ou même choisir une valeur personnalisée dans une cellule qui peut avoir été produite par une formule statistique.
Excel est un outil idéal pour l'analyse statistique et le reporting. Fournit de nombreuses alternatives pour calculer l'incertitude afin que vous obteniez ce dont vous avez besoin.
setTimeout(fonction(){
!fonction(F,b,e,v,m,t,s)
{si(f.fbq)revenir;n=f.fbq=fonction(){n.callMethod?
n.callMethod.apply(m,arguments):n.queue.push(arguments)};
si(!f._fbq)f._fbq=n;n.push=n;n.chargé=!0;n.version=’2.0′;
n.queue=[];t=b.createElement(e);t.async=!0;
t.src=v;s=b.getElementsByTagName(e)[0];
s.parentNode.insertAvant(t,s) } (window, document,'scénario',
'https://connect.facebook.net/en_US/fbevents.js’);
fbq('init', « 335401813750447 »);
fbq('Piste', « Page View »);
},3000);